# Functional Data Structures

# Defining Functional Data Structures

A functional data structure is operated on using only pure functions.

A pure function is a function that does not mutate data and performs no side effects.

Consider the following functional data structure, a singly linked list:

sealed trait List[+A]
case object Nil extends List[Nothing]
case class Cons[+A](head: A, tail: List[A]) extends List[A]

object List {
  def sum(ints: List[Int]): Int = ints match {
    case Nil => 0
    case Cons(x, xs) => x + sum(xs)
  }

  def product(ds: List[Double]): Double = ds match {
    case Nil => 1.0
    case Cons(0.0, _) => 0.0
    case Cons(x, xs) => x * product(xs)
  }

  def apply[A](as: A*): List[A] =
    if (as.isEmpty) Nil
    else Cons(as.head, apply(as.tail: _*))
}

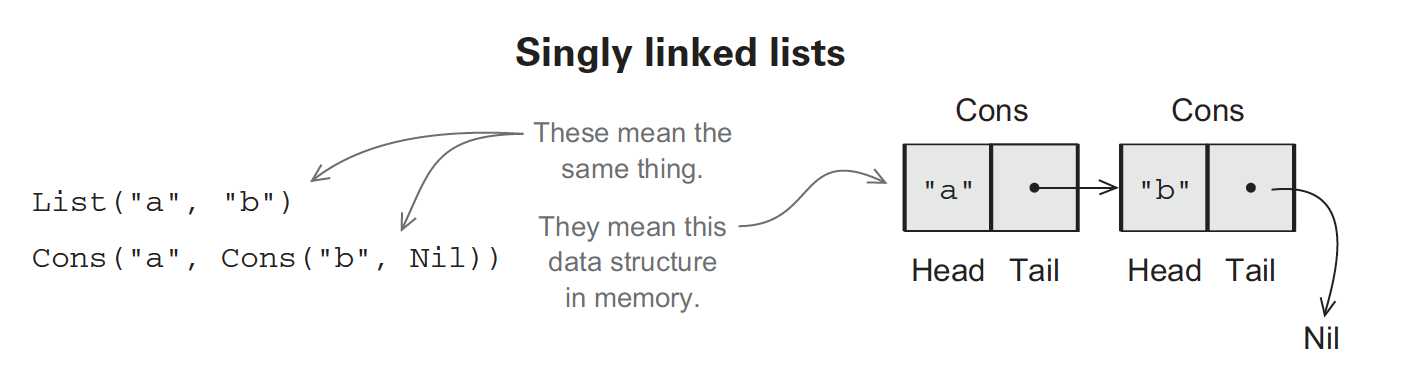
• A trait is an abstract interface that may optionally contain implementations of some methods.
  • Here the trait List is defined, without any methods.
• The sealed keyword enforces that all implementations of the trait must be declared in this file.
• The lines that start with case are the two implementations or data constructors of List.
  • These implementations show the two forms List can take.
  • Nil represents an empty list.
  • Cons represents a nonempty list, which consists of a head and a (possibly empty) list tail of the remaining elements.

The type parameter [+A] declared after List indicates that List is polymorphic (similar to how functions can be polymorphic).

# Type Variance

The + declared before the A in [+A] indicates that A is covariant.

• This means that if X is a subtype of Y, then List[X] is a subtype of List[Y].
• Nothing is a subtype of all types. This covariance allows us to write List[Double] and declare it to Nil with no problems.

# Variadic Functions

The apply function in object List is a variadic function as it accepts an arbitrary number of As as its arguments.

• The _* part of the recursive call to apply returns the rest of the arguments.

function apply(...as) {
  if (as.length === 0) return []
  return [as[0], apply(as.slice(1))]
}

# Companion Objects

A companion object is an object with the same name and data type as our declared data type (In the code snippet above, it is the object List declaration).

• The companion object contains various convenience functions for working with values of the data type.

# Pattern Matching

sum and product in the List object above makes use of pattern matching:

def sum(ints: List[Int]): Int = ints match {
  case Nil => 0
  case Cons(x, xs) => x + sum(xs)
}

Pattern matching is essentially a more powerful switch statement. The pattern in the match statement are more "flexible" than in switches:

List(1, 2, 3) match { case _ => 42 }

• Returns 42.
  • _ is known as a variable pattern. Any variable (like x or foo) can be used here but it's convention to use _.

List(1, 2, 3) match { case Cons(h, _) => h }

• Returns 1.
  • This is because the List is basically Cons(1, Cons(2, Cons(3, Nil))), so the _ matches the tail portion of the first Cons.

List(1, 2, 3) match { case Nil => 42 }

• Results in a MatchError because none of the cases matched the target.

# Data Sharing

We can reuse parts of our data structure when manipulating it. This avoids us having to copy our entire data structure to maintain immutability.

• To add an element to an existing list, say xs, we simply do Cons(x, xs).
• To remove the first element, we just return the tail.

# Fold

The sum and product functions do somewhat similar things; it returns a value if the List is Nil, and does some operation if it's not.

This can be generalized into the foldRight function:

def foldRight[A, B](as: List[A], z: B)(f: (A, B) => B): B =
  as match {
    case Nil => z
    case Cons(x, xs) => f(x, foldRight(xs, z)(f))
  }

We can then define sum in terms of foldRight:

def sum2(ns: List[Int]) =
  foldRight(ns, 0)((x, y) => x + y)